RUMUS-RUMUS INTEGRAL KALKULUS II
mempunyai suku konstanta sembarang.
1.2 Rumus-rumus Integral Tak Tentu
1.3 Definisi Integral Tentu
sebagai berikut:
maka menurut dalil pokok dari kalkulus integral, integral tentu diatas dapat dihitung dengan
rumus :
1.4 Rumus-rumus Integral tentu
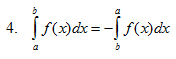

dengan k sebagai konstanta sembarang.

1.5 Integral Parsial
Prinsip dasar integral parsial :
- Salah satunya dimisalkan U
- Sisinya yang lain (termasuk dx) dianggap sebagai dv
Sehingga bentuk integral parsial adalah sebagai berikut :



1.1 Beberapa Aplikasi dari Integral
a. Perhitungan Luas suatu kurva terhadap sumbu x



b. Menghitung luas diantara dua buah kurva

c. Menghitung volume benda putar yang diputar terhadap sumbu koordinat












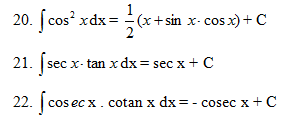







Tidak ada komentar :
Posting Komentar